Simulate Stark effect for linear molecule OCS
The problem of linear molecule rotation in the presence of static electric field can be solved easily using ready analytical expressions for the matrix elements of dipole moment. For linear molecule, the laboratory-frame \((X,Y,Z)\) and molecular-frame \((x,y,z)\) projections of dipole moment are related as \(\mu_Z=\cos(\theta)\mu_z\), where \(\theta\) is the Euler angle. From the properties of spherical harmonics, obtain \(\cos(\theta)=2\sqrt{\pi/3}Y_{1,0}\). Thus, the total Hamiltonian for linear molecule in static electric field, oriented along \(Z\) axis, can be written as
\begin{align}
H=BJ^2-2\sqrt{\pi/3}Y_{1,0}\mu_z F_Z.
\end{align}
We solve the Schrödinger equation using variational method, i.e., by expanding the total wave function as linear combination of basis functions, which are eigenfunctions of Hamiltonian \(H_0 = BJ^2\) describing field-free rotation of linear molecule. It is well known that eigenfunctions of \(J^2\) operator are spherical harmonics \(Y_{J,m}\).
The matrix representation of \(H\) in the basis of spherical harmonics is
\begin{align}
\langle Y_{J',m'}|H| Y_{J,m}\rangle = BJ(J+1)\delta_{J,J'}\delta_{m,m'} - 2\sqrt{\pi/3}\mu_z F_Z\langle Y_{J',m'}|Y_{1,0}| Y_{J,m}\rangle.
\end{align}
Using the product rule for spherical harmonics, obtain
\begin{align}
\langle Y_{J',m'}|Y_{1,0}| Y_{J,m}\rangle = (-1)^{m'}\sqrt{\frac{(2J'+1)(2J+1)(2+1)}{4\pi}}
\left(\begin{array}{ccc}J'&1&J\\-m'&0&m\end{array}\right)
\left(\begin{array}{ccc}J'&1&J\\0&0&0\end{array}\right).
\end{align}
The code below implements it
[8]:
import numpy as np
from sympy.physics.wigner import wigner_3j
B = 0.203 # in cm^-1
dz = 0.55 # in Debye
fz = 10000 # in V/cm
conv_to_cm = 1.679201682918921e-05 # converts dz[Debye]*Fz[V/cm] into cm^-1
# note on unit conversion: Debye = 1/c * 10^{-21} Coulomb*meter and Coulomb*Volt = Joule
energy = lambda J: B*J*(J+1)
costheta_me = lambda J1, m1, J2, m2: 2*np.sqrt(np.pi/3.0) * (-1)**m1 * np.sqrt((2*J1+1)*(2*J2+1)*3/(4*np.pi)) \
* wigner_3j(J1, 1, J2, -m1, 0, m2) * wigner_3j(J1, 1, J2, 0, 0, 0)
Jmax = 10
Jm_quanta = [(J, m) for J in range(Jmax+1) for m in range(-J, J+1)]
H0 = np.diag([energy(J) for (J,m) in Jm_quanta])
H = np.array([[costheta_me(J1, m1, J2, m2) for (J1, m1) in Jm_quanta] for (J2, m2) in Jm_quanta], dtype=np.float64)
Htot = H0 - H * dz * fz * conv_to_cm
enr, vec = np.linalg.eigh(Htot)
print(enr)
[-6.91681529e-03 4.03902042e-01 4.03902042e-01 4.10113514e-01
1.21699992e+00 1.21699992e+00 1.21849733e+00 1.21849733e+00
1.21900241e+00 2.43541649e+00 2.43541649e+00 2.43599970e+00
2.43599970e+00 2.43635009e+00 2.43635009e+00 2.43646697e+00
4.05961804e+00 4.05961804e+00 4.05990445e+00 4.05990445e+00
4.06010910e+00 4.06010910e+00 4.06023192e+00 4.06023192e+00
4.06027286e+00 6.08973066e+00 6.08973066e+00 6.08989225e+00
6.08989225e+00 6.09001794e+00 6.09001794e+00 6.09010773e+00
6.09010773e+00 6.09016161e+00 6.09016161e+00 6.09017957e+00
8.52579992e+00 8.52579992e+00 8.52589995e+00 8.52589995e+00
8.52598181e+00 8.52598181e+00 8.52604547e+00 8.52604547e+00
8.52609095e+00 8.52609095e+00 8.52611823e+00 8.52611823e+00
8.52612733e+00 1.13678455e+01 1.13678455e+01 1.13679117e+01
1.13679117e+01 1.13679677e+01 1.13679677e+01 1.13680136e+01
1.13680136e+01 1.13680492e+01 1.13680492e+01 1.13680747e+01
1.13680747e+01 1.13680900e+01 1.13680900e+01 1.13680951e+01
1.46158771e+01 1.46158771e+01 1.46159232e+01 1.46159232e+01
1.46159631e+01 1.46159631e+01 1.46159969e+01 1.46159969e+01
1.46160246e+01 1.46160246e+01 1.46160461e+01 1.46160461e+01
1.46160614e+01 1.46160614e+01 1.46160706e+01 1.46160706e+01
1.46160737e+01 1.82699000e+01 1.82699000e+01 1.82699333e+01
1.82699333e+01 1.82699627e+01 1.82699627e+01 1.82699882e+01
1.82699882e+01 1.82700098e+01 1.82700098e+01 1.82700275e+01
1.82700275e+01 1.82700412e+01 1.82700412e+01 1.82700510e+01
1.82700510e+01 1.82700569e+01 1.82700569e+01 1.82700589e+01
2.23300000e+01 2.23300000e+01 2.23301000e+01 2.23301000e+01
2.23301895e+01 2.23301895e+01 2.23302685e+01 2.23302685e+01
2.23303370e+01 2.23303370e+01 2.23303949e+01 2.23303949e+01
2.23304423e+01 2.23304423e+01 2.23304791e+01 2.23304791e+01
2.23305054e+01 2.23305054e+01 2.23305212e+01 2.23305212e+01
2.23305265e+01]
Let’s repeat the above calculations for different values of field and plot the Stark curves - state energies versus field
[9]:
import matplotlib.pyplot as plt
stark = []
for fz in np.linspace(0, 10, 100): # field in kV
#print("do fz =", fz, "kV/cm ...")
Htot = H0 - H * dz * fz*1000 * conv_to_cm
enr, vec = np.linalg.eigh(Htot)
stark.append([fz, *enr])
stark = np.array(stark)
plt.plot(stark[:,0], stark[:,2])
plt.plot(stark[:,0], stark[:,3])
plt.plot(stark[:,0], stark[:,4])
[9]:
[<matplotlib.lines.Line2D at 0x7f004c9e4b00>]
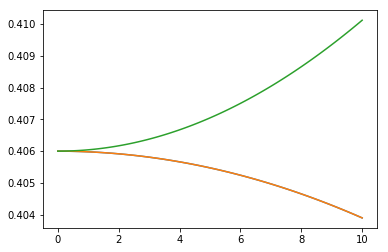
We can now run same calculations using watie and extfield
[10]:
# First, compute and store in file rotational energies and matrix elements of dipole moment operator
from richmol.watie import RigidMolecule, SymtopBasis, JJ, CartTensor
import numpy as np
#######################################################################
# OCS rotational energies and richmol matrix elements of dipole moment
# using ab initio values computed at CCSD(T)/ACVQZ level of theory
#######################################################################
ocs = RigidMolecule()
ocs.XYZ = ("angstrom",
"C", 0.0, 0.0, -0.522939783141,
"O", 0.0, 0.0, -1.680839357,
"S", 0.0, 0.0, 1.037160128)
ocs.tensor = ("dipole moment", [0, 0, -0.31093])
#ocs.frame = "pas"
Bx, By, Bz = ocs.B
print("rotational constants:", Bx, By, Bz)
# compute rotational energies for J = 0..10
Jmax = 10
wavefunc = {}
for J in range(Jmax + 1):
bas = SymtopBasis(J, linear=True)
H = Bx * JJ(bas) # linear molecule Hamiltonian
hmat = bas.overlap(H)
enr, vec = np.linalg.eigh(hmat.real)
wavefunc[J] = bas.rotate(krot=(vec.T, enr))
# store rotational energies
for J in range(Jmax + 1):
wavefunc[J].store_richmol("ocs_j0_j"+str(Jmax)+".h5")
mu = CartTensor(ocs.tensor["dipole moment"], name='mu', units='au', descr="ab initio CCSD(T)/ACVQZ")
# compute and store matrix elements of dipole moment
for J1 in range(Jmax + 1):
for J2 in range(J1, Jmax + 1):
if abs(J1 - J2) > 1: continue # selection rules
mu.store_richmol(wavefunc[J1], wavefunc[J2], "ocs_j0_j"+str(Jmax)+".h5", thresh=1e-10)
/home/andrey/.local/lib/python3.6/site-packages/richmol-0.1a1-py3.6.egg/richmol/watie.py:305: RuntimeWarning: divide by zero encountered in double_scalars
return [convert_to_cm/val for val in np.diag(imom)]
rotational constants: 0.203439376816691 0.203439376816691 inf
[11]:
# Load field-free data and compute field-dressed states
from richmol.extfield import States, Tensor, Hamiltonian, mu_au_to_Cm, planck, c_vac
from richmol import rchm
Jmax = 10
richmol_file = "ocs_j0_j10.h5"
# field-free states
states = States(richmol_file, 'h0', [J for J in range(Jmax + 1)], emin=0, emax=10000)
# dipole matrix elements
mu = Tensor(richmol_file, 'mu', states, states)
mu.mul(-1.0)
stark = []
for Fz in np.linspace(0.1, 10, 100): # field in kV
#print("do fz =", Fz, "kV/cm ...")
field = [0, 0, Fz * 1000 *100] # field in V/m
# multiply dipole with external field
mu2 = mu * field
# convert dipole[au]*field[V/m] into [cm^-1]
fac = mu_au_to_Cm / (planck * c_vac) / 100.0
mu2.mul(fac)
# combine -dipole*field with field-free Hamiltonian
ham = Hamiltonian(mu=mu2, h0=states)
# matrix representation of Hamiltonian
hmat = ham.tomat(form='full')
# eigenvalues and eigenvectors
enr, vec = np.linalg.eigh(hmat)
stark.append([Fz, *enr])
stark = np.array(stark)
plt.plot(stark[:,0], stark[:,2])
plt.plot(stark[:,0], stark[:,3])
plt.plot(stark[:,0], stark[:,4])
[11]:
[<matplotlib.lines.Line2D at 0x7f004e73e668>]
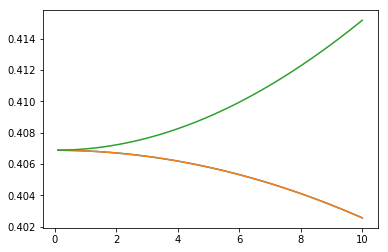
Note, these results are expected to be slightly different from those above because of the differences in rotational \(B\) constant and dipole moment.
[ ]: